项目

1、数据
2、过拟合处理方式
3、模型更新

八股文

1、xgboost原理
2、线性回归三种区别正则化
3、rmse、R^2区别

编程

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。
图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。
每个 顶点对 由 最多一条 边连接，并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。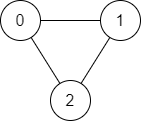


输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:

  • 0 → 1 → 2
  • 0 → 2
    </pre>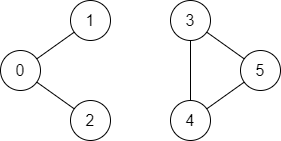 
    输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    n = 3
    edges = [[0,1],[1,2],[2,0]]
    s = 0
    d = 2
    # n = 6
    # edges = [[0,1],[0,2],[3,5],[5,4],[4,3]]
    # s = 0
    # d = 5

    matrix = [[0]*n for i in range(n)]
    for x,y in edges:
        matrix[x][y] = 1
        matrix[y][x] = 1

    def dfs(x,y,flag):
        if x==y or matrix[x][y]:
            return True
        else:
            for z in range(n):
                if not(flag >> z) and matrix[x][z]:
                    falg = flag | 1 << z
                    dfs(z, y ,flag)
                    falg = flag & ~(1 << z)
            return False
        
    def bfs(x,y,flag):
        if x==y or matrix[x][y]:
            return True
        else:
            from queue import Queue
            q = Queue()
            q.put(x)
            while not q.empty():
                source = q.get()
                for z in range(n):
                    if not(flag >> z) and matrix[source][z]:
                        q.put(z)
                        falg = flag | 1 << z
                        if z == y:
                            return True
            return False
     
    def Find(x:int):
        if fa[x]!=x:
            #路径压缩
            fa[x] = Find(fa[x])
        return fa[x]
       
    def union(x:int,y:int):
        a = Find(x)
        b = Find(y)
        if a < b :
            fa[b] = a 
        else:
            fa[a] = b

    # 并查集代码
    #初始化
    fa = [i for i in range(n)]
    for x,y in edges:
        union(x,y)
    print(Find(s)==Find(d))
    print(dfs(s,d,1 << n-1-s))
    print(bfs(s,d,1 << n-1-s))

    位运算(https://leetcode.cn/circle/discuss/CaOJ45/)