Flash Attention on INTEL GPU - 知乎

Excerpt
来源：https://zhuanlan.zhihu.com/p/607364156

之前是业余看论文写了这篇FlashAttention的介绍，后面team也在做LLM上的优化了，我刚好负责的是kernel的优化，于是花了一个多月的时间，针对intel的GPU实现了FlashAttention，这期间多了很多感悟，所以把文章更新…

之前是业余看论文写了这篇FlashAttention的介绍，后面team也在做LLM上的优化了，我刚好负责的是kernel的优化，于是花了一个多月的时间，针对intel的GPU实现了FlashAttention，这期间多了很多感悟，所以把文章更新下。

自从2017年谷歌DeepMind推出Transformer模型^[1]，Transformer便取代了RNN模型，成为了NLP领域的Top。如今大火的Bert，GPT系列，以及Stable-Diffusion都是基于Transformer。Transformer的核心是self-attention机制，这也是它区别于RNN的地方，能够一次处理所有的输入数据，而不是像RNN那样一次处理一个，解决了长期依赖问题，也有利于并行。

Transformer模型的训练对硬件的要求往往很高，因为其基本模块，multi-head attention(MHA)的时间复杂度和空间复杂度都是 O(N2) ， N 表示sequence length。所以，对于sequence length比较大的模型，MHA的内存开销和性能都容易成为瓶颈。

标准MHA

先来看下标准的MHA的实现。

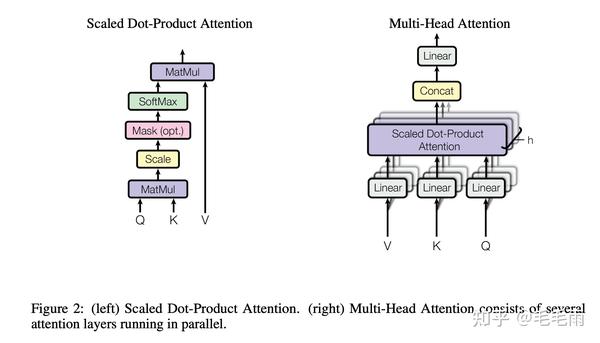
给定 Q,K,V, shape为(BatchSize, NumHead, SeqLen, HeadDim), 基本公式如下：

output\=softmax(QKT∗scale)V

其中Softmax的计算是row-wise的，需要计算整行的max/sum，所以整个计算往往是分成了三步。

S\=QKT∗scale
P\=Softmax(S)
O\=PV

P 是internal buffer, size = BatchSize x NumHead x SeqLen x SeqLen。

从标准的MHA出发，比较naive的GPU实现是分成3个kernel，第一个是gemm，第二个是point-wise，第三个是gemm，依次执行，这种naive实现的问题有两个，1 是内存开销大，因为需要存储中间结果S/P，这两个都是 O(N2) ，随着现在模型的sequence length越搞越大，这个内存要求是很高的。 2 是性能问题，在长sequence length的情况下，S/P不能塞到cache里，这样每次读取都是从HBM读，这样latency就比较长。

常见的解法是算子融合。

下面我们来试试，如果想把第二步的softmax融合到第一个gemm，由于softmax是对整行求sum/max，这和gemm常见的tiling策略其实是冲突的，所以融合softmax就对第一个gemm的block切分加上了限制，要么行方向不切，减少并行度，要么做类似k-slicing，增加communication的成本。同理，如果想把这三个融合到一个kernel，不改变softmax计算的前提下，总是要在前面说的两种方法中取一个balance。

这样的做法可以，但是很显然不是最佳solution，尤其是在batch比较小，而sequence length又比较长的case下。那么我们能不能把封印解除呢？融合softmax，但是也还是能做tiling？那就是搞个lazy softmax，分步计算，这其实就接近作者提出的flash attention了^[2]。

这个思路是写kernel比较自然的优化思路。我们也可以抛开实现，从问题本身来分析，先看下MHA的算术密集度（arithmetic intensity）。

用 N 表示SeqLen, D 表示HeadDim，先来算下memory operations，这里按理想情况考虑（有一块无穷大的cache），至少需要从HBM 读取 3ND (包括Q/K/V), 写入 ND (指output），总共是 4ND。再来算下compute operations，忽略中间的softmax的计算，应该是 2∗2N2D , 第一个2是表示前后共有两个GEMM，第二个2是表示每次计算是2个操作，mul和add，那么arithmetic intensity \=4N2D4ND\=N , 可以认为是compute bound。

所以，之前有不少工作致力于减少MAH中的计算量，比如sparse，或者low-rank，降到甚至 O(N) 的复杂度，但是模型的E2E performance却没有得到很大的提升，而且由于这两种方法都会降低精度，也都没有被广泛采用。究其原因，作者认为是没有考虑memory access(IO)的overhead。这里就需要说下hardware的特性了，拿NVIDIA的A100 40GB PCIe举例^[3]，FP16的flops是312T，而HBM的bandwdith是1,555GB/s，也就是说每从HBM读取一个FP16，至少需要进行 312∗1e121555∗1e9/sizeof(float16)\=401 次运算，才能用满TensorCore，这个要求无疑是非常高的，所以实际上，由于TensorCore的计算速度远高于HBM的load/store速度，如果不能把数据保存在latency更低的cache里（比如A100的L1/SLM），问题往往是受限于I/O，而不是compute。

那问题就落在怎么把数据放cache里？标准的回答是tiling，那softmax怎么tiling？又回到了这个问题。

我认为FlashAttention算法的核心便是softmax的tiling。下面就具体来看下这个：

对于标准MHA的实现，这里摘一段stable-diffusion的代码供参考^[4]：

class CrossAttention(keras.layers.Layer):
    def __init__(self, n_heads, d_head):
        super().__init__()
        self.to_q = keras.layers.Dense(n_heads * d_head, use_bias=False)
        self.to_k = keras.layers.Dense(n_heads * d_head, use_bias=False)
        self.to_v = keras.layers.Dense(n_heads * d_head, use_bias=False)
        self.scale = d_head**-0.5
        self.num_heads = n_heads
        self.head_size = d_head
        self.to_out = [keras.layers.Dense(n_heads * d_head)]

    def call(self, inputs):
        assert type(inputs) is list
        if len(inputs) == 1:
            inputs = inputs + [None]
        x, context = inputs
        context = x if context is None else context
        q, k, v = self.to_q(x), self.to_k(context), self.to_v(context)
        assert len(x.shape) == 3
        q = tf.reshape(q, (-1, x.shape[1], self.num_heads, self.head_size))
        k = tf.reshape(k, (-1, context.shape[1], self.num_heads, self.head_size))
        v = tf.reshape(v, (-1, context.shape[1], self.num_heads, self.head_size))

        q = keras.layers.Permute((2, 1, 3))(q)  # (bs, num_heads, time, head_size)
        k = keras.layers.Permute((2, 3, 1))(k)  # (bs, num_heads, head_size, time)
        v = keras.layers.Permute((2, 1, 3))(v)  # (bs, num_heads, time, head_size)

        score = td_dot(q, k) * self.scale
        weights = keras.activations.softmax(score)  # (bs, num_heads, time, time)
        attention = td_dot(weights, v)
        attention = keras.layers.Permute((2, 1, 3))(
            attention
        )  # (bs, time, num_heads, head_size)
        h_ = tf.reshape(attention, (-1, x.shape[1], self.num_heads * self.head_size))
        return apply_seq(h_, self.to_out)

Tiling for softmax

回顾下Softmax的公式（一般sofmtax都会加上最大值的处理，主要是为了数值稳定，避免直接计算指数导致数值溢出）。

m(x)\=max(xi),softmax(xi)\=exi−m(x)∑0iexi−m(x)

因为Softmax需要拿到每一行的max/sum，所以一般来说，我们需要等某一行的数据全部ready之后，才进行Softmax操作。那能不能做tiling呢？当然可以，不就是算个max/sum，每次保存当前的max/sum，再逐步更新，最后得到的结果不是一样吗？

假设我们要对数组[x_0, x_1…x_n]进行softmax处理，先处理第一个数

cur_max = x_0
cur_sum = exp(x_0 - cur_max)
score = exp(x_0 - cur_max) / cur_sum
pre_max = cur_max
pre_sum = cur_sum

然后算第二个数的结果

1
2
3

cur_max = max(pre_max, x_1)
cur_sum = pre_sum * (exp(pre_max - cur_max) + exp(x_1 - cur_max)
score = exp(x_1 - cur_max) / cur_sum

这个过程中，pre_max/pre_sum被不断更新，这样就可以逐步的计算Softmax了，而不用等到每一行的输入都ready。再把这里的每个数扩充成一个block，那就是tiling了，和前面的gemm完美契合。

Softmax + GEMM

回到MHA，现在有了softmax的tile，那么softmax接在第一个gemm后面就很自然，当普通的post-op处理就可以。复杂一点的地方是，softmax后面gemm，逐步计算中，每次softmax的结果并不是正确的，那如何保证后一个gemm拿到的结果是正确的呢？关键的一点在于，softmax分tile后得到的局部的“错误”的值，这个scale因子，对于整行的所有元素是一样的，都是exp(-max)/sum, 所以只需要在下一次计算除以这个scale，去掉上次错误的影响，累计到最后就是正确的结果了。

Talk is cheap, show me the code, 下面是一份简单的python实现

import numpy as np

f = 16
t = 16
h = 8

q = np.random.random(size=(f, h))
k = np.random.random(size=(t, h))
v = np.random.random(size=(t, h))
do = np.random.random(size=(f, h))
head_scale = 1 / np.sqrt(float(h))
dropout_prob = 0.3
dropout_mask = np.random.random(size=(f, t)) >= dropout_prob


def dropout(array, ratio, mask):
    assert (array.shape == mask.shape)
    scale = 1 / (1 - float(ratio))
    array_dp = array * scale
    zero = np.zeros(array.shape, dtype=array.dtype)
    output = np.where(mask, array_dp, zero)
    return output


def flash_attention(q, k, v, is_train=False):
    output = np.zeros(q.shape, dtype=np.float32)
    m = np.zeros(f, dtype=np.float32)
    l = np.zeros(f, dtype=np.float32)

    block_m = 2
    block_n = 2
    block_head = h
    assert (f % block_m == 0)
    assert (t % block_n == 0)
    for start_m in range(0, f, block_m):
        m_prev = np.zeros([block_m], dtype=np.float32) - float("inf")
        l_prev = np.zeros([block_m], dtype=np.float32)
        acc = np.zeros([block_m, block_head], dtype=np.float32)
        q_sub = q[start_m: start_m + block_m, :]
        for start_n in range(0, t, block_n):
            k_sub = k[start_n: start_n+block_n, :]
            v_sub = v[start_n: start_n+block_n, :]
            dropout_mask_sub = dropout_mask[start_m: start_m +
                                            block_m, start_n: start_n+block_n]
            qk = np.matmul(q_sub, k_sub.T)
            qk *= head_scale
            m_cur = np.maximum(np.amax(qk, -1), m_prev)
            l_prev *= np.exp(m_prev - m_cur)
            p = np.exp(qk - m_cur.reshape(-1, 1))
            l_cur = np.sum(p, -1) + l_prev
            l_rcp = 1 / l_cur
            s = p * l_rcp.reshape(-1, 1)
            acc *= (l_prev * l_rcp).reshape(-1, 1)
            # Below commeneted part is from flash attention2
            # s = p
            # acc *= np.exp(m_prev - m_cur).reshape(-1, 1)
            dp_s = dropout(s, dropout_prob, dropout_mask_sub)
            acc += np.matmul(dp_s, v_sub)
            m_prev = m_cur
            l_prev = l_cur
        # acc /= l_prev.reshape(-1, 1)
        output[start_m: start_m+block_m, :] = acc
        m[start_m: start_m+block_m] = m_prev
        l[start_m: start_m+block_m] = l_prev

    if is_train:
        return output, m, l
    else:
        return output


def naive_attention(q, k, v, is_train=False):
    score = np.matmul(q, k.T)
    score *= head_scale
    row_max = np.amax(score, -1).reshape(-1, 1)
    row_sum = np.sum(np.exp(score - row_max), -1).reshape(-1, 1)
    prob = np.exp(score - row_max) / row_sum
    prob_dp = dropout(prob, dropout_prob, dropout_mask)
    output = np.matmul(prob_dp, v)
    if is_train:
        return output, prob, prob_dp
    else:
        return output


def forward_test(q, k, v):
    desired = naive_attention(q, k, v)
    actual = flash_attention(q, k, v)
    np.testing.assert_allclose(actual, desired, rtol=1e-5, atol=1e-5)

再回头对比下Flash attention，由于softmax的tiling处理，gemm/softmax/gemm三步被很好的融合到一起，这样既省掉了中间buffer(S/P)的开销，又能方便地把数据放cache，一举两得地解决了之前标准MHA的两个问题。

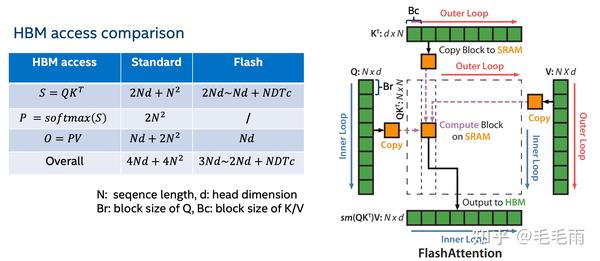
理解了算法的基本思路，下一步就是，怎么在intel的硬件上实现一个高效的GPUkernel呢？

Flash Attention GPU Kernel的实现

基本框架

整个MHA的逻辑可以写成如下的伪代码：

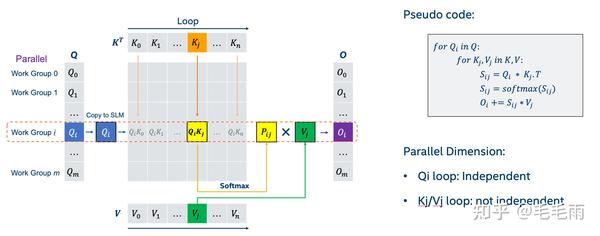
先考虑怎么切分，首先batch和num_head这两个维度是可以并行的，其次不同Q_i的计算是完全独立的，所以很自然Q的方向也可以做parallel。那要不要切分K/V呢，这就主要考虑occupancy，看前面已经并行的维度能不能把整个硬件塞满，比如intel的数据中心GPU，PVC，一个tile一共有64 XeCore。而在通常LLM的case里，batch(>=1) x num_head(>=16) x num_beam(4) * parallel_q(>=1)是大于64的，能够塞满整个PVC的一个tile，在这种情况下，如果切分K/V，额外的通信开销就是没必要的，所以我目前的kernel实现没有对K/V进行切分。注：这里说的num_beam是beam search。

考虑了怎么切分，接下来就可以开始着手写了。我这边是基于intel的一个library：XeTLA实现的，这个library可以看作是intel的cutlass，是一个主要针对gemm的模板库，提供了高性能的micro kernel，比如device/workgroup/subgroup level的brgemm。具体代码上传到了intel extension for tensorflow 这个仓库里，感兴趣的同学可以看看。

preload Q

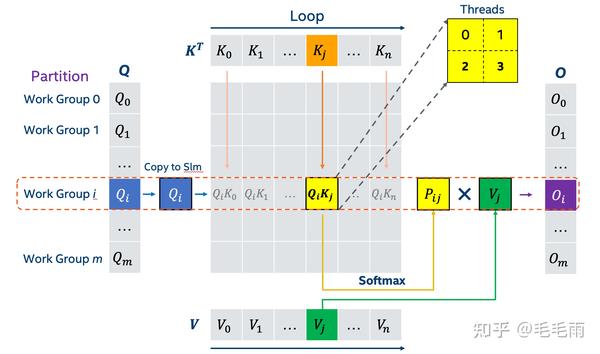
按照前面说的切分，每个workgroup会计算上图的一块 QiKj ，workgroup内部的threads则进一步切分 QiKj ，所以workgroup内不同的thread会share同一份 Qi ，为了避免反复从HBM读取，代码里做了一个preload Q的优化，把当前workgroup 需要的那一小块Q从HBM提前load到shared local memory, 这样可以被整个workgroup share，达到对Q的快速读取。

优化softmax

softmax本质上是reduction，所以套用reduction的常用优化，分成好几个block，先block内部做，然后再block之间做。

按照上图的划分，也就是theads0和thread1先做各自的gemm，然后各自做softmax，最后再整合。这样做的好处是减少同步，每个thread做完gemm就可以接着做softmax，而不需要等待其他的thread。

causal mask

causal mask是decoder里需要的，依照上述pytorch官方的定义，是把第一个gemm的结果的上三角结果置为-inf, 实现上我直接省掉了上三角的所有计算，这样理论上是可以拿到最高2x的性能提升的。

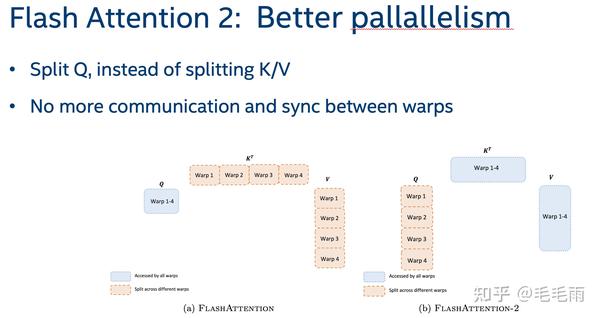
Flash Attention 2

Flash Attention 2出来的时候我马上就看了论文^[5]，但看完以后有点失望，觉得idea不算很新。总结下来是2点，1是减少了non-matmul的计算，2是更高的并行度。

第一点，从forward的角度看是对Bc的loop里，每次少了一个division，从backward的角度看，减少了中间buffer的大小，不需要m/l都存，只需要一个m了。

第二点，更好的并行，在Q的维度上加了并行，其实这个思路应该是非常自然的。在Flash attention2出来以前，pytorch2.0里sdp的实现就是这样进行切分的，所以没啥特别。

Flash Attention For LLM

回到如今大火的LLM，对于inference的场景，由于kv cache的优化，从second token开始，每次是输入一个token，也就意味着模型里的MHA中的query的sequence length是等于1的。而大部分gpu的systolic array的设计，比如cuda的tensor core，至少计算一个8x16的矩阵才能拿到满的throughput，intel的pvc的xmx单元也类似，要求大小至少是8x16。所以m=1实际上是一个计算上的浪费，为了解决这个问题，FasterTransformer里提出了一个新的solution，把问题看成reduction，而不是gemm，用FPU来算，而不是systolic array。我也针对这个实现了一版，实测下来，发现对于inference case性能确实是可以的，因为计算量不大，用FPU还是systolic array区别不大。

写在最后

最后的一点感慨是关于tiling的，flash attention本质上我觉得是解决了softmax的tiling问题，而tiling是为了适配GEMM的，但我们一定要用tiling来解决GEMM相关的问题吗？有没有其他solution。